二十年以来对 RSA 密码系统攻击综述

RSA攻击汇总

0.引入

这篇文章翻译自Dan Boneh的Twenty Years of Attacks on the RSA Cryptosystem，其中部分译文参考了二十年以来对 RSA 密码系统攻击综述 (seebug.org)~~（但是这个译文机翻有点重，而且公式也没有了）~~。希望通过这篇文章，对目前常见的RSA攻击进行一个总结以及较为深入的了解。

1.分解大整数(Factoring Large Integers)

我们将模分解称为对RSA的暴力攻击。尽管因数分解算法一直在改进，但在正确使用RSA时，目前的技术水平，还远远没有对RSA的安全性构成威胁。虽然大整数的因式分解是计算数学中最美丽的问题之一，但它不是本文的主题。

目前最快的分解算法是General Number Field Sieve(普通数域筛选法)，其时间复杂度为

学长在服务器上操作下来情况是这样的：16核32线程分解400bits的n，需要4000s；分解505bits的n，需要67小时。

开放性问题1：给定整数n和e，满足gcd(e, phi(n))=1。定义函数 $f_{e,n}:Z^*_n\to Z^*_n,\ f_{e,n}(x)=x^{\frac{1}{e}}\pmod n$ ，是否存在一个多项式时间的算法A，对于给定n，可以计算n的分解同时能访问一些e的oracle $f_{e,n}(x)$ 。

有学者指出，上述开放性问题，对于一个较小的e来说，答案是否定的。

下面我们将证明知道公开私钥 d 和分解 N 是等效的。因此，对于知道 d 的任何一方隐藏 N 的因式分解是没有意义的。

分解n显然可以很容易计算得到d。
若给定d，我们有 $k=e*d-1$ ，通过定义我们可以知道，k是 $\phi (n)$ 的倍数，我们知道 $\phi(n)$ 是偶数，同时有 $k=2^t*r$ ，（ $r$ 是奇数）。对于 $g\in Z^*_n$ ，有 $g^k\equiv1\pmod n$ ，并且 $g^{\frac{k}{2}}$ 是模n的平方根，由中国剩余定理我们知道，对于n=p*q，这样的数有4个。其中，有两个是正负一，还有两个是 $\pm x$ ，其中 $x\equiv1\pmod p,x\equiv-1\pmod q$ 。使用后两者，我们就可以通过计算gcd(x-1, n)得到n的分解。有简单的论证表明，如果g是在 $Z^*_n$ 中随机取，那么序列 $g^{\frac{k}{2}},g^{\frac{k}{4}},\dots,g^{\frac{k}{2^t}}\pmod n$ 的其中一个是平方根且能分解n的概率至少为1/2。序列中的所有元素都可以在 $O(\log_2{n})^3)$ 的时间内有效计算。

2.两种简单攻击

2.1共模攻击

共模攻击是一种只需要知道多组公钥对，就可以推出明文的攻击，在上一篇中已经介绍，这里就不再赘述。

2.2Blinding——盲签名（攻击）

令<n,d>为私钥，<n,e>为公钥。我们想让Bob对m签名，Bob肯定会拒绝。于是我们选择一个随机数 $r\in Z_n^*$ ，并且令 $M'=r^em$ ，明文改变了，Bob可能愿意在看上去没什么问题的M’上签名。但是此时，我们就可以很简单的得到原本的签名 $S'\equiv(M')^d\pmod n,\ S\equiv S'/r\pmod n$ 。

不过由于大多数签名方案在签名之前对消息应用"单向散列"算法，这种攻击并不是一个严重的问题。况且，正如标题中攻击在括号里一样，这种盲签名在区块链中应用更广。

3.低解密指数攻击

为了减少解密时间（或签名时间），人们希望使用一个较小的d，而不是随机的d。而这种操作就会导致下面的一些攻击。

定理(M. Wiener)：令 $n=pq$ ，且 $q<p<2q，d<\frac{1}{3}n^{\frac{1}{4}}$ ，如果给定公钥，我们可以有效恢复解密指数d。
证明：我们有等式 $ed-k\phi(n)=1$ ，于是

此时， $\frac{k}{d}$ 是 $\frac{e}{\phi(n)}$ 的近似值。尽管我们不知道 $\phi(n)$ ，但是我们可以用n近似它。

同时，由p、q的不等关系容易得到 $p+q-1<3\sqrt n$ ，于是

我们用上面的不等式代换原有的等式

由于等式 $k\phi(n)=ed-1<ed$ ，因为 $e<\phi(n)$ ，根据不等式原则可以知道 $k<d<\frac{1}{3}n^{\frac{1}{4}}$ 。于是，上面的不等式可以进一步得到

这是一个经典的逼近关系，分数 $\frac{k}{d}$ 且 $k<n$ 在约束 $\log_2n$ 内非常逼近 $\frac{e}{n}$ 。实际上，所有类似这样的分数都是的连分数展开的收敛。因此我们首要做的便是计算的连分数 $\frac{e}{n}$ 的收敛，其中一个连分数就等于 $\frac{k}{d}$ 。由于 $ed − kϕ(N)=1$ ，所以 $gcd(k,d)=1$ ，因此 $\frac{k}{d}$ 是一个最简分数。这就是一个可以算出密钥d的线性时间算法。

Wiener attack后来被 Boneh and Durfee两人改进，把d的界扩大到了 $d<n^{0.292}$ ，这样的结果表明Wiener的界限并不固定。正确的界限可能是 $d<n^{0.5}$ 。不过截至到这篇paper发表的时间，这还是一个尚未解决的问题。

开放性问题2：令 $n=pq，d<n^{0.5}$ ，如果给定满足RSA的e、d，是否可以有效的恢复d？

4.低加密指数

为了减少加密或签名验证时间，通常会使用一个小的公钥指数。e的最小可能值为3，但为防止某些攻击，一般推荐使用 $e=2^{16}+1=65537$ 。当使用e=65537时，签名验证需要17次乘法运算，而使用随机的e时则需要大约1000次乘法运算。与上一节的攻击不同，当使用一个小e时，应用的攻击不仅仅是得到明文而已。

4.1 Coppersmith’s Theorem

针对RSA低公钥指数最有力的攻击是基于Copper-smith的一个定理，Coppersmith定理有很多应用，这里我们只讨论其中的一些应用，具体如下。

定理(Coppersmith)：令n为一个整数， $f\in Z[x]$ 是d次的一元多项式，设 $X=N^{\frac{1}{d}-\epsilon}$ 其中 $\epsilon\geq0$ ，在给定 $<n,f>$ 之后Marvin能够有效找到所有满足 $|x_0|<X$ 的整数，运行时间由在维数为 $O(w)$ 且 $w=min(1/\epsilon,\log_2N)$ 的格上运行的LLL算法所需时间决定。

该定理为有效地求模 $N$ 的所有小于 $X=N^{1/d}$ 的根提供了一种算法，当X越小，算法的运行时间越短。这个定理的强大之处在于它能够找到多项式的小根。当模数为素数时，就目前而言，找不到比使用Coppersmith定理更好的求根算法。

我们概述了Coppersmith定理证明背后的主要思想，我们采用由Howgrave-Graham提出的简化方法。给定多项式 $h(x)=\Sigma a_ix^i\in Z[x]$ ，并定义 $||h||^2=\Sigma|a_i|^2$ 。证明需要下面的引理。

引理：令 $h(x)\in Z[x]$ 是d次多项式，同时令X为正整数。假设 $||h(xX)||<N/\sqrt d$ ，如果存在 $|x_0|<X$ 满足 $h(x_0)=0\pmod N$ ，那么 $h(x_0)=0$ 对整数成立。
证明：从Schwarz不等式观察到：

因为 $h(x_0)=0\pmod N$ ，所以我们可以得到结论。

引理指出，如果 $h$ 是一个低范数多项式，则 $h\pmod N$ 的所有小根也是 $h$ 在整数上的根。引理表明，要找到 $f(x)\pmod N$ 的一个小根 $x_0$ ，我们需要寻找另一个和 $f\pmod N$ 有相同根的低范数多项式 $h\in Z[x]$ ，这样就能容易找到在 $h$ 整数上的根 $x_0$ 。为此，我们可以寻找一个多项式 $g\in Z[x]$ ，使得 $h=gf$ 具有低范数，即范数小于 $N$ 。这相当于寻找具有低范数多项式的整数线性组合 $f,xf,x^2f,\dots,x^rf$ 。不过，大多数情况下，并不存在具有足够小的范数的非平凡线性组合。

Coppersmith找到了解决这个问题的方法：如果 $f(x_0)\equiv 0\pmod N$ 成立，那么对于任意 $k$ 则有 $f(x_0)^k\equiv 0\pmod {N^k}$ 。更一般地，定义以下多项式：

对于给定m，有

对任意 $u\geq0,0\leq v\leq m$ ，则 $x_0$ 是 $g_{u,v}(x)\pmod {N^m}$ 的一个根。

要使用引理4，我们必须找到多项式 $g_{u,v}(x)$ 的一个整数线性组合 $h(x)$ ，使得 $h(xX)$ 的范数小于 $N^m$ (回想一下 $X$ 是满足 $X\leq N^{1/d}$ 的 $x_0$ 的上界)。由于范数（是 $N$ 而不是 $N^m$ ）的松弛上界，我们可以证明，对于足够大的 $m$ ，总是存在一个线性组合 $h(x)$ 满足所要求的界。一旦 $h(x)$ 被找到，引理4就说明它有整数根 $x_0$ ，于是， $x_0$ 就可以很容易地找到。

如何有效地找到 $h(x)$ 还有待证明，要做到这一点，我们必须先陈述一些关于格的基本事实。设是 $u_1,\dots,u_w\in Z^w$ 线性独立的向量。由 $<u_1,\dots,u_w>$ 构成的(满秩)格是 $u_1,\dots,u_w$ 的所有整数线性组合的集合。 $L$ 的行列式定义为w×w方阵的行列式，其行向量是 $u_1,\dots,u_w$ 。

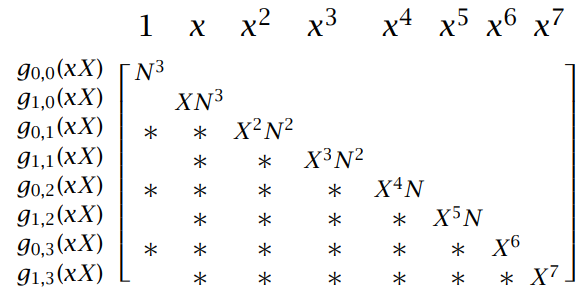
在我们的例子中，我们把多项式 $g_{u,v}(xX)$ 看作向量，并研究了它们所构成的格L。设 $v=0,\dots,m$ ， $u=0,\dots,d-1$ ，则格的维数为 $w=d(m+1)$ 。例如，当 $f$ 是二次一元多项式且 $m=3$ 时，得到以下的格：

$*$ 元素对应我们忽略的其值的多项式的系数，所有空元素为零。由于矩阵是三角阵，其行列式就是对角线元素乘积。我们需要在这个格中找到短向量。

Hermite的一个经典结论表明：任意维数为 $w$ 的格 $L$ 包含一个非零向量 $v\in L$ ，它的范数满足 $||v||\leq \gamma_w\det(L)^{1/w}$ ，其中 $\gamma_w$ 是只依赖于 $w$ 的常数。Hermite的界可以用来证明，对于足够大的 $m$ ，我们的格包含小于的范数 $N^m$ 向量。问题是我们能否有效地在中构造长度小于Hermite界的短向量，而LLL算法恰好是一种有效的算法。

Fact（LLL）：若格 $L$ 有一组基 $<u_1,\dots,u_w>$ ，通过LLL算法，可以得到一个向量 $v\in L$ 满足：

算法的运行时间是输入长度的四分之一

通过LLL算法，我们就可以完成Coppersmith定理的证明。为了保证LLL算法产生的向量满足引理4的界，我们需要满足：

其中 $w=d(m+1)$ 是 $L$ 的维度。常规计算表明，对于足够大的 $m$ ，也能满足约束条件。实际上，当时 $X=N^{\frac{1}{d}-\epsilon}$ ，取 $m=O(k/d)$ 和 $k=\min(\frac{1}{\epsilon},\log N)$ 就足够了。因此，运行时间主要由在维数为 $O(k)$ 的格上运行LLL算法所决定。

一个自然而然的问题，Coppersmith定理能否应用于二元和多元多项式。如果 $f(x,y)\in Z_N[x,y]$ 有根 $(x_0,y_0)$ 且 $|x_0y_0|$ 有适当的界，我们能有效地找到 $(x_0,y_0)$ 吗？尽管相同的技术似乎仍然适用于某些二元多项式，但它目前还是一个有待证明的开放性问题。随着越来越多的结果依赖于Coppersmith定理的二元扩展，严密的算法将会非常有用。

开放性问题3：找出可以将 Coppersmith 定理推广到二元多项式的一般条件。

4.2 Hastad广播攻击

其简化版本就是国内常说的低加密指数广播攻击，直接CRT然后开三次方就可以得到明文。一般来说，需要收集k组密文， $k\geq e$ 。

Hastad提出了一种更强的攻击方法。为了抵御上述的攻击，发送方会做一些简单的防御。Bob在加密之前"填充"消息，而不是直接广播加密后的 $M$ 。例如，如果 $M$ 是m位长的，Bob可以将 $M_i=i2^m+M$ 发送给party $P_i$ 。由于我们获得了不同消息的加密，就无法发起上述攻击。然而，Hastad证明了这种线性填充是不安全的，事实上，他证明了在加密之前对消息应用任何固定多项式都不能阻止攻击。

假设对于每个参与者 $P_1,\dots,P_k$ ，Bob有一个固定的公用多项式 $f_i\in Z_{N_i}[x]$ 。为了广播消息 $M$ ，Bob将 $f_i(M)$ 的加密发送给party $P_i$ 。我们通过窃听知道了 $C_i\equiv f_i(M)^{e_i}\pmod N_i$ ，其中 $i=1,\dots,k$ 。Hastad证明，如果有足够的参与方，我们就可以从所有的密文中恢复出明文。以下定理是Hastad原始结论的一个更强的版本。

定理6（Hastad）：令 $N_1,\dots,N_k$ 是两两互质的整数，并设 $N_{\min}=\min_i(N_i)$ 。设 $g_i\in Z_{N_i}$ 是 $k$ 个 $d$ 次多项式。假设存在唯一的 $M<N_{\min}$ 满足

假设 $k>d$ ，给定 $<N_i,g_i>_{i=1}^k$ ，我们就可以很容易恢复 $M$ 。

这个定理表明，当提供了足够多的方程，我们就可以有效地求解以两两互素的整数为模的单变量方程组。令 $g_i\equiv f_i^{e_i}-C_i\pmod {N_i}$ ，当有至少 $d$ 组数据时，我们就可以恢复 $M$ 了。特别的，如果所有的e都一样并且Bob发送线性相关的消息，那么我们只要 $k(k>e)$ 组数据，就可以算出明文。

Hastad的原始定理比上述定理更弱。与 $d$ 次多项式不同，Hastad定理需要 $d(d+1)/2$ 次多项式。Hastad定理的证明类似于上一节中提到的Coppersmith定理证明。然而，Hastad 格中没有使用 $g$ 的幂，因此得到了一个较弱的界。

总结这一部分，我们注意到，要正确地防御上述广播攻击，必须使用随机填充方法，而不是使用固定填充方法。

4.3 Franklin-Reiter相关消息攻击

当Bob用相同的模数发送与Alice相关的加密消息时，Franklin和Reiter发现了一种巧妙的攻击。 $<N,e>$ 是Alice的公钥，假设 $M_1,M_2\in Z_N^*$ 是两个不同的消息，但存在一个已知的多项式 $f\in Z_N[x]$ ，满足 $M_1=f(M_2)$ 。为了将 $M_1,M_2$ 发送给Alice，Bob可能会简单地对消息进行加密，并发送得到的密文 $C_1,C_2$ 。通过证明可以知道，在给定 $C_1,C_2$ 的情况下，我们可以很容易地计算出 $M_1,M_2$ 。虽然攻击对任意小 $e$ 都有效，但为了简化证明，我们给出了 $e=3$ 时的引理。

引理（FR）：令 $e=3$ ， $<N,e>$ 是RSA的公钥，且对于 $M_1\ne M_2\in Z_N^*$ ，存在一个线性多项式 $f=ax+b\in Z_N[x]\ \ (b\ne0)$ 满足 $M_1=f(M_2)\pmod N$ 。于是，给定 $<N,e,C_1,C_2,f>$ ，我们就可以在 $(\log N)^2$ 的时间内恢复 $M_1,M_2$ 。
证明：为了保证这部分证明的一般性，我们使用任意的 $e$ 来表示它（而不是局限在 $e=3$ ）。由于 $C_1\equiv M_1^e\pmod N$ ，我们可以知道 $M_2$ 是多项式 $g_1(x)=f(x)^e-C_1\in Z_N[x]$ 的一个根。同样的， $M_2$ 也是 $g_2(x)=x^e-C_2\in Z_N[x]$ 的一个根。这两个多项式都有同一个线性因子 $x-M_2$ ，因此我们就可以计算 $\gcd(g_1,g_2)$ ，如果结果是线性的，那么我们就找到了 $M_2$ 。

我们证明了当 $e=3$ 时，GCD的结果一定是线性的。多项式因子 $x^3-C_2$ 将 $p,q$ 都模成一个线性因子和一个不可约二次因子(因为 $\gcd(e,\phi(N))=1$ ，所以 $x^3-C_2$ 在 $Z_N$ 中只有一个根)。因为 $g_2$ 不能整除 $g_1$ ，所以GCD一定是线性的。对于 $e>3$ 的情况，GCD几乎总是线性的。然而，对于一些罕见的 $M_1,M_2$ 和 $f$ ，有可能得到一个非线性的GCD，在这种情况下攻击会失败。

对于 $e>3$ 情况，攻击所需时间是 $e$ 的平方。因此，只有在使用小的公钥指数 $e$ 时才能应用这种攻击。对于大 $e$ ，计算GCD的工作令人望而却步。为任意 $e$ 设计这样的攻击是一个有趣的问题（尽管可能很困难）。特别是，上面 $g1$ 和 $g2$ 的GCD能否在 $\log e$ 的多项式时间内找到吗？

4.4 Coppersmith短填充攻击

Franklin-Reiter的攻击可能看起来有点人为。毕竟，为什么Bob要给Alice发送相关消息的加密呢？Coppersmith加强了攻击，并证明了一个关于填充攻击的重要的结论。

一个简单的随机填充算法可能会通过将几个随机位附加到一个末端来填充一个明文 $M$ ，但是以下攻击指出了这种简单填充的危险。假设Bob向Alice发送了正确填充的加密 $M$ 。攻击者Marvin拦截密文并阻止其到达目的地。Bob注意到Alice没有回复他的消息，并决定将重新发送给Alice。他随机填充并传输生成的密文 $M$ 。Marvin现在有两个密文，对应于使用两种不同随机填充对同一消息的两次加密。以下定理表明，虽然他不知道使用的填充算法，但Marvin仍能够算出明文。

定理8：令 $<N,e>$ 是RSA的公钥，N长为 $n$ -bits。令 $m=[n/e^2]$ ，设 $M\in Z_N^*$ 是长最多为 $n-m$ -bits的消息。定义 $M_1=2^mM+r_1,M_2=2^mM+r_2$ ，其中 $r_1,r_2$ 是不同的整数，且 $0\leq r_1,r_2\leq 2^m$ 。如果给定 $<N,e>$ 和密文 $C_1,C_2$ ，那么就可以有效恢复 $M$ 。
证明：定义 $g_1(x,y)=x^e-C_1,g_2(x,y)=(x+y)^e-C_2$ 。我们知道，当 $y=r_2-r_1$ 时，两个多项式有共同的根 $M_1$ 。也就是说， $\Delta=r_2-r_1$ 是结果 $h(y)=res_x(g_1,g_2)\in Z_N[y]$ 的根。 $h$ 的次数最多为 $e^2$ 。此外，有 $|\Delta|<2^m<N^{1/e^2}$ ，因此 $\Delta$ 是 $h\pmod N$ 的一个小根，所以我们就可以通过Coppersmith定理计算它。一旦 $\Delta$ 求出来，Franklin-Reiter攻击就可以用来计算 $M_2$ ，最终算出 $M$ 。

当 e = 3 时，只要填充长度小于消息长度的 1/9，就可以发起攻击。这是一个重要的结论。但是需要注意，对于 e = 65537 这一推荐值，对于标准的模数大小来说，这种攻击就无效了。

4.5 部分密钥泄露攻击

设 $<N,d>$ 为RSA私钥，假设Marvin通过某种方式知道了 $d$ 的一部分，比如说 $d$ 的四分之一比特。他能得到 $d$ 剩下的部分吗？当相应的公钥指数很小时，答案是肯定的。最近，Boneh，Durfee和Frankel证明了只要 $e<\sqrt N$ ，就有可能从它的一小部分位算出的所有部分。这个结论说明了保护整个RSA私钥的重要性。

定理9(BDF)：令 $<N,d>$ 是RSA的私钥，其中 $N$ 有n比特。当给定 $[n/4]$ 个最低有效位，Marvin可以在 $e\log_2e$ 的线性时间内恢复所有d。
定理10(Coppersmith)：令 $N=pq$ 是n比特的RSA模数，给定 $p$ 的 $n/4$ 个最低有效位或 $p$ 的 $n/4$ 个最高有效位，我们就可以有效分解 $N$ 。

定理9很容易从定理10推出来，事实上，对于 $e,d$ 有：

由于 $d<\phi(N)$ ，可以知道 $0<k\leq e$ ，对方程模 $2^{n/4}$ 进行约化，令 $q=N/p$ ，我们得到

由于我们知道 $d$ 的低 $n/4$ 的值，于是就有 $ed\pmod{2^{n/4}}$ 的值。我们就可以得到一个关于k和p的等式，对于每一个e对应k的可能值，我们求解上面的方程，获得 $p\pmod{2^{n/4}}$ 的候选值。对于这些候选值，应用定理10的算法分解N。而所有候选值的总数最多为 $e\log_2e$ ，因此在遍历这些值后，N就被成功分解。

定理9被称为部分密钥泄露攻击，对于更大 $e$ 的值，只要 $e<\sqrt N$ ，也存在类似的攻击，不过，要实现此种攻击的技术有点复杂。有趣的是，基于离散对数的密码系统，如ELGamal公钥系统，似乎不容易受到部分密钥泄漏攻击的影响。事实上，如果给出 $g^x\pmod p$ 和 $x$ 位的常数分数，则没有已知的多项式时间算法来计算 $x$ 的其余部分。

为了总结这一节，我们将证明当加密指数 $e$ 很小时，RSA系统会泄漏相应私钥 $d$ 一半的最高有效位。要了解这一点，再考虑一个方程 $ed-k(N-p-q+1)=1$ ，其中 $0<k\leq e$ 。给定 $k$ ，Marvin可以很容易地计算出：

然后

因此 $\hat{d}$ 是 $d$ 的很好的近似值。上面的界表明，对于大多数 $d$ ， $\hat{d}$ 的一半高位和d中的相同。由于只有 $e$ 个可能的 $k$ ，因此Marvin可以构造一个大小为 $e$ 的集合，使得该集合中的一个元素等于 d 的最高有效位的一半。 $e=3$ 的情况特别有趣，在这种情况下，可以证明总是 k = 2，因此系统完全泄漏了 d 的一半最高有效位。

5. 执行攻击

我们将注意力转向完全不同的攻击类别。这些攻击不是攻击 RSA 函数的底层结构，而是侧重于 RSA 的实现。

5.1 时序攻击 (Timing Attacks)

想象有一个存储RSA私钥的智能卡，由于这张卡为了防止篡改，所以Marvin可能不能检查其中的内容，从而直接得到的密钥。但是有一个Kocher想到了一个巧妙的攻击方式：通过精确地测量这张卡执行RSA解密（或签名）所需的时间，可以快速找到私钥d。

下面，我们将解释如何使用"重复平方算法"，对一个简单的RSA实现进行攻击。令 $d=d_{n}d_{n-1}\dots{}d_{0}$ ，其中后半部分是d的二进制表示，即 $d=\Sigma_{i=0}^{n}2^{i}d_{i},\ \ d_{i}\in{}\lbrace1,2\rbrace$ 。模重复平方法在对 $C\equiv{}M^{d}\pmod{N}$ 进行计算时，最多进行2n次乘法。算法具体如下：

令 $z=M,C=1$ ，对于 $i=0,1\dots{},n$ ，进行如下操作
1. 如果 $d_{i}=1$ ，令 $C\equiv{}C*z\pmod{N}$
2. 令 $z\equiv{}z^2\pmod{N}$

对于 $i=0,1\dots{},n$ ，变量 $z$ 遍历值 $M^{2^i}\pmod{N}$ 的集合，变量 $C$ 在集合中"收集"合适的幂以得到结果。

为了发起攻击，Marvin需要智能卡对大量随机消息 $M_{1},\dots{},M_{k}\in{}Z_{N}^{*}$ 生成签名，并测量每个签名生成所需的时间 $T_{i}$ 。

攻击从 $d$ 的最低有效位开始，逐个算出每个比特位。我们知道 $d$ 是奇数，因此 $d_0=1$ 。考虑第二次迭代： $z\equiv{M^{2}}\pmod{N},C=M$ 。如果 $d_1=1$ ，则智能卡会计算 $Cz=M$ ，否则，它是不进行这一步运算。设 $t_i$ 是智能卡计算 $M_i*M_i^2\pmod{N}$ 所花费的时间。由于计算 $M_i*M_i^2\pmod{N}$ 的时间取决于 $M_i$ 的值，因此 $t_i$ 彼此不同（简单模约化算法需要不同的时间，具体取决于被归约的值）。一旦Marvin获得智能卡的物理规格，他就可以离线测量得到 $\lbrace{t_i}\rbrace$ （在发起攻击之前）。

Kocher观察到当 $d_1=1$ 时，两个集合 $\{t_i\}$ 和 $\{T_i\}$ 是相关的。例如，如果对于某些 $i$ ，比预期的 $t_i$ 要大得多，那么 $T_i$ 也可能大于预期。另一方面，如果 $d_1=0$ ，则两个集合 $\{t_i\}$ 和 $\{T_i\}$ 表现为独立的随机变量。通过测量相关性，Marvin可以确定是0还是1。继续使用这个方法，他可以很快得到 $d_2,d_3$ 等等。注意到当使用低公钥指数时，上一节的部分密钥泄露攻击表明，使用Kocher的时序攻击，只需要知道 $d$ 的四分之一位就行。

有两种方法可以抵御攻击。最简单的是添加适当的延迟，以使模幂运算总是要花费一定的时间。第二种方法是由Rivest提出的基于盲化的方法。在解密 $M$ 之前，智能卡选择一个随机的 $r\in{Z_N^*}$ 并计算 $M'=M*r^e$ ，然后将 $d$ 应用于上 $M'$ 并获得 $C'\equiv{(M')^d\pmod{N}}$ ，最后，令 $C\equiv{C'/r\pmod{N}}$ 。通过这种方法，将 $d$ 应用于Marvin不知道的随机消息 $M'$ 上，这样的话，Marvin就不能发起攻击了。

Kocher最近在这些线路上发现了另一种叫做功率密码分析的攻击。 Kocher表明，通过在签名生成过程中精确测量智能卡的功耗，Marvin通常可以轻松发现密钥。事实证明，在多精度乘法期间，卡的功耗高于正常值。通过测量高消耗周期的长度，Marvin可以很容易地确定在给定的迭代中卡是执行一次还是两次乘法，从而暴露出的比特位。

Kocher最近发现了另一种类似的攻击，称为能量分析攻击。Kocher指出通过精确测量智能卡在签名生成过程中的功耗，Marvin通常可以很容易地得到秘密密钥。结果表明，在多精度乘法过程中卡的功耗会高于正常值，通过测量高消耗周期的长度，Marvin可以很容易地确定在给定的迭代中，卡执行一次还是两次乘法，从而得到 $d$ 的比特位。

5.2 随机故障 (Random Faults)

RSA的解密和签名的实现经常使用中国剩余定理来加速 $M^d\pmod{N}$ 的计算，签名者Bob为了替换模N，先计算签名模p和q的结果，然后利用中国剩余定理将结果结合起来。更准确地说，Bob首先计算：

其中 $d_p\equiv{d\pmod{p-1}},d_q\equiv{d\pmod{q-1}}$ 。然后令：

其中：

与两次求幂相比，CRT最后一步的运行时间可以忽略不计。p和q的长度是N的一半，由于简单的乘法实现需要平方时间，所以模p的乘法速度是模n的4倍，而且 $d_p$ 是 $d$ 的一半长，于是计算 $M^{d_p}\pmod{p}$ 的速度是计算 $M^{d}\pmod{n}$ 的8倍，因此，整个签名时间减少了四倍，许多实现都使用这种方法来提高性能。

Boneh，DeMillo和Lipton观察到使用CRT方法有内在的危险。假设在生成签名时，Bob的计算机上的一个小故障导致它在一条指令中错误计算。例如，在将寄存器中的值从一个位置复制到另一个位置时，其中一个比特位被翻转了。(故障可能是由环境电磁干扰引起的，也可能是由于罕见的硬件缺陷造成的，比如早期版本的奔腾芯片。)

Marvin得到了无效的签名给定之后可以很容易地对Bob的模数进行分解。

正如A. K. Lenstra所说，我们发现了一个新的攻击。假设在Bob生成签名时发生一个错误，那么， $C_p$ 或 $C_q$ 中将有一个被错误地计算。如果说 $C_p$ 是正确的，那么就 $\hat{C_q}$ 会不正确，得到的签名为 $\hat{C}=T_1C_p+T_2\hat{C_q}$ 。一旦Marvin获取到了 $\hat{C}$ ，通过计算 $\hat{C^e}\neq{M\pmod{N}}$ ，他就知道这是一个错误的签名。然而注意到：

因此， $\gcd{(N,\hat{C^e}-M)}$ 便是n的一个非平凡因子。

要使攻击奏效，Marvin必须对 $M$ 有充分的了解。也就是说，我们假设Bob不使用任何随机填充方法，签名前的随机填充可以防御此种攻击，对于Bob来说，一个更简单的防御方法是在将生成的签名发送给全世界之前检查生成的签名。当使用CRT加速方法时，检查是特别重要的。随机故障攻击对许多密码系统都是有害的，许多系统，包括RSA的非CRT实现，都可以使用随机故障进行攻击。不过，这些结论更多的是理论性的。

5.3 Bleichenbacher对PKCS 1的攻击 (Bleichenbacher’s Attack on PKCS 1)

设 $N$ 是n-位的RSA模， $M$ 是m-位消息，其中 $m<n$ 。在应用RSA加密之前，一般会通过向其添加随机比特，将 $M$ 填充到n位。公钥加密标准1（Public Key Cryptography Standard 1, PKCS 1）的旧版标准就是使用的这种方法。填充后，消息如下所示：

生成的消息长度为n位，并直接使用RSA加密。包含"02"的初始块长度为16位，从上图可看出已在消息中添加了随机填充。

当Bob的机器接收到PKCS 1消息时，应用程序(例如，Web浏览器)会对其进行解密，检查初始块，并去掉随机填充。但是，一些应用程序会检查"02"初始块，如果不存在，就会返回一条错误消息，报错"无效密文"。Bleichenbacher表示这个错误消息可能导致灾难性的后果：攻击者Marvin可以使用错误消息解密他所选择的密文。

假设Marvin截获了一个针对Bob的密文 $C$ ，并希望对其进行解密。为了发起攻击，Marvin随机挑选了一个 $r\in{Z_N^*}$ ，计算 $C'\equiv{rC\pmod{N}}$ ，并将 $C'$ 发送到Bob的机器。运行在Bob的机器上的应用程序接收并尝试解密它。它要么用错误消息进行响应，要么根本不响应(如果的格式正确的话)。因此，Marvin知道解密过程中16位最高有效位是否等于02。实际上，Marvin有这样的oracle，对于他选择的任何 $r$ ，他都可以测试解密 $rC\pmod{N}$ 的16位最高有效位是否等于02。Bleichenbacher证明了这样的oracle足以解密 $C$ 。