Intro
差分密码分析是一种密码分析的方法,主要用于破解分组加密,但也适用于流加密和加密哈希函数。而差分分析的首次提出,是针对Feal-4算法,所以本篇会先从Feal-4加密算法讲起,然后再介绍其在DES、AES中的应用。
Feal-4加密算法
Feal-4密码算法在密码学史上有很重要的地位,差分攻击正是研究者通过对Feal-4的研究首次提出的,之后又拓展到了DES密码算法上。自此以后,抗差分分析成了密码设计的一部分,差分分析成为了密码分析的基本方法。
由于Feal-4的自身的设计特点,差分攻击对Feal-4非常有效,不需要大量的选择明文就可以实现。
Feal-4加解密流程
Feal-4属于分组加密算法,采用Feistel架构。密钥长度为8字节,分组长度也是8字节。
Feal-4密码算法对一个分组的加密过程可用下图概述:
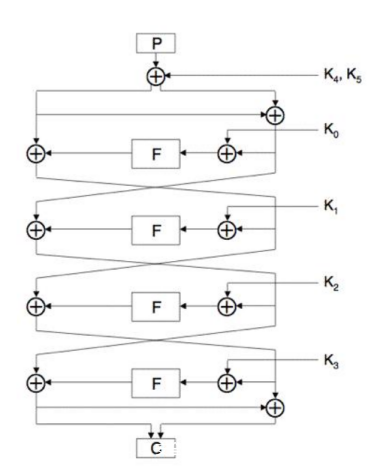
首先,8字节的密钥经过子密钥生成算法,扩展为6个4字节的子密钥 K0 – K5,加密过程使用的就是这样6个4字节子密钥。所以如果能恢复出子密钥,不需要恢复原始密钥,就能完成对Feal-4的解密,下文的差分攻击也正是这样做的。
分组加密过程中,首先8字节明文分组被分成左右两个部分,左半部与子密钥K4异或,右半部与子密钥K5异或。两个半部再异或作为右半部。接着进入4轮轮函数。每一轮里,右半部直接成为下一轮的左半部。这和DES比较类似。
第一轮里,右半部与K0异或,然后进入F函数,F函数实现非线性部分,F函数的结果与左半部进行异或,成为下一轮的右半部。后3轮同理,依次使用子密钥 K1 K2 K3。
4轮操作完成后,左半部就是密文分组的左半部,左半部与右半部异或后,成为密文分组的右半部。这就是一个分组的加密过程。
而解密过程,就是上述过程的逆过程。
轮函数
下面我们来看F函数。Feal-4的脆弱性就在F函数中。轮函数F将32比特映射为32比特。轮函数中使用了一个名为G函数的操作,G函数有两个定义如下
这里的移位是循环移位
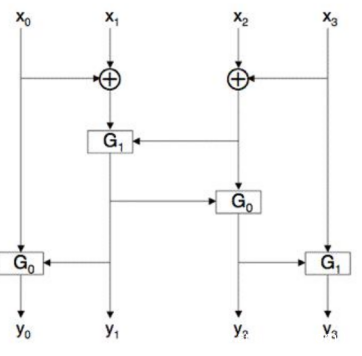
有了G函数,我们看一下轮函数内部
对Feal-4进行差分攻击
差分分析的目标是获得子密钥。差分分析最早由Murphy于1990年,针对Feal4密码提出,随后 Biham 和 Shamir 又在一系列研究里对该技术进行了发展,属于选择明文攻击,适用于过度使用异或操作的分组密码算法。
差分分析,是指追踪明文对的差异的传播。这里的差异由我们根据目标定义,可以是异或值,也可以是别的。而对于Feal-4,差异指的就是异或值。
-
定义:差分特征(differential characteristic)
选定明文分组P1,分组之间的“差值”(differential)为δ,于是另一个明文分组就是P1+δ,明文P1对应的密文分组时C1,明文 P1+δ 对应的密文与C1的“距离”是 ε
若 δ 以一定概率对应着 ε,就称 δ 是一个差分特征
对于上述过程,也可以用下图描述
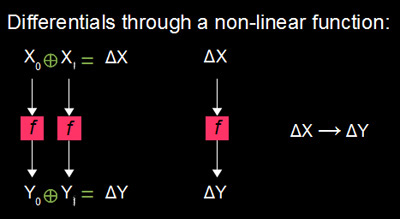
在Feal-4密码里,有这样两个有用的“特征”
- 同样的输入经过轮函数F一定产生同样的输出,即,当轮函数的输入差值为0x00000000时,轮函数的输出差值一定为0x00000000,概率为1。
- 当轮函数的输入差值为0x80800000时,轮函数的输出差值一定为0x02000000,概率为1。
基于这两个事实,我们来追踪差分特征0x8080000080800000在Feal-4加密过程的传播。
我们可以任意选择一个明文分组P0,然后与0x8080000080800000异或,得到明文分组P1,P0与P1构成一个明文对,差值为0x8080000080800000, 对应的密文分组分别是C0和C1,记
我们把
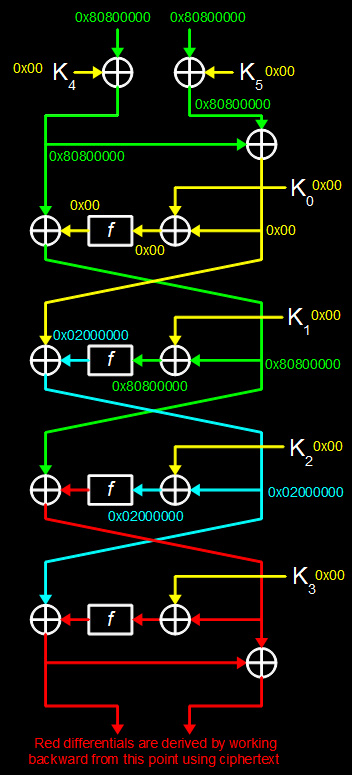
上述差值进入后,我们可以看到在第三轮,也就是绿色箭头停止的地方,在这之前输出对于我们都是已知的,而这之后,由于0x02000000对应的轮函数差值不确定,我们不能继续追踪了。
我们记第三轮0x02000000进入f函数后得到的输出是
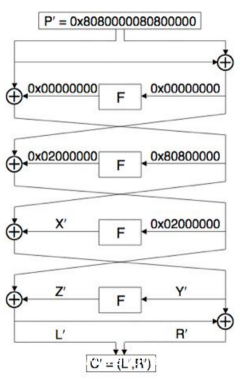
由于
于是整个流程中的所有数我们现在都知道了,下面就需要得到子密钥,完成整个分析。
结合实际加密流程,我们需要通过枚举K3,计算Z0和Z1,从而获得实际的Z0^Z1
通过上面的计算,我们把
然后就可以模仿刚才的方式,通过枚举得到K2,其差分特征是0x0000000080800000。最后可以通过差分特征0x00000000 02000000 求解出K1。
但是我们此时并不知道K0,K4,K5。注意到只有K0参与了和上面类似情况的加密过程,所以我们采取和上面类似的方式获得K0,用差分特征0x00000000 02000000。由于有了K3,K2,K1,我们就可以得到第一轮加密的左右输出,记为L1’、R1’,于是
同时,我们枚举K0,得到
于是我们同样可以得到关于K0的等式,判断方法和前面一样。在找到K0后,得到未加密的左右输出,只需要进行异或就可以得到K4,K5。
Sum
本篇通过Feal-4算法初步介绍了差分攻击,由于内容实在太多,其余内容会在后续几篇介绍。
- reference:
- 由Feal-4密码算法浅谈差分攻击 - 安全客,安全资讯平台 (anquanke.com)
- The Amazing King - Differential Cryptanalysis of FEAL




Comments NOTHING