在上一篇中,我们介绍了DES。在DES被提出后,针对它密码强度的批评主要在以下两个方面:
- DES的密钥空间太小,易受到蛮力攻击
- DES S盒的设计准则是保密的,所以有可能已经存在利用S盒数学属性的分析攻击,只是这种攻击只有DES的设计者知道
除了DES外,还存在许多其他的分组密码。比如AES,3DES。3DES有两种版本:
尽管3DES能够抵抗当前技术发起的蛮力攻击,但是它仍然存在一些问题。比如,由于DES本身就不适合软件实现,那么3DES实现的时间就是DES需要时间的三倍多。于是就有了我们本篇要学习的AES算法。
AES算法
AES算法支持的密钥大小为128、192、256位。这里只讨论密钥大小为128位的AES算法,其加密轮数为10轮,192位的轮数为12轮,256位的轮数位14轮。
下图是加密的简要过程
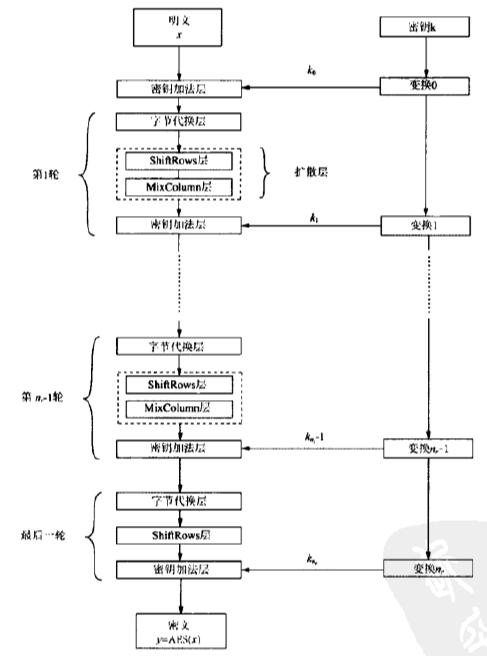
除了最后一轮不一样,每轮加密包括了
-
字节变换层(S-盒) :同DES中S-盒功能类似
-
扩散层:扩散层中包含两个子层,每个子层都执行线性操作。
- ShiftRows(行移位变化)层
- MixColumn(列混淆变换)层
-
密钥加法层:密钥和状态异或
下图是每轮的具体过程图
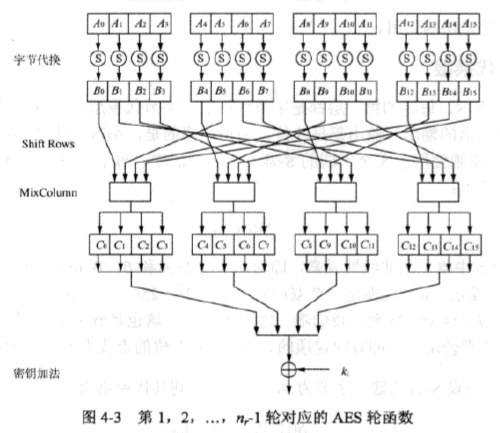
字节变换层
这一层可以看作是16个并行的S-盒,其输入和输出都是8位,AES中使用的S-盒是完全相同的。S-盒如下表
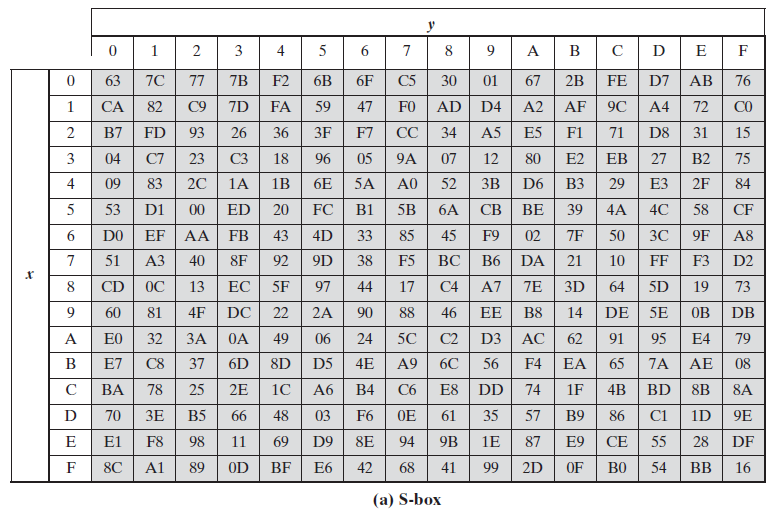
明文的一个字节由8位组成,以这8位的高4位作为S盒表的行值,低4位作为S盒表的列值。在其中寻找对应的代替结果。例如:十六进制数0x3F表示代替结果在第三行,第F列,因此结果为0x75。
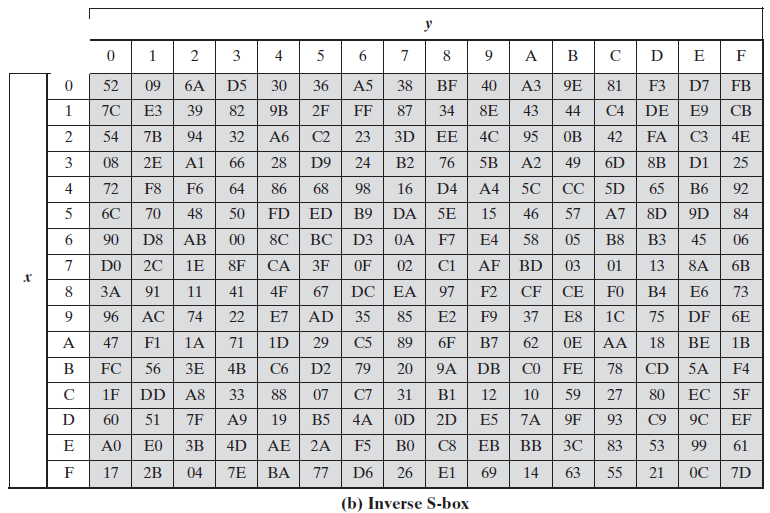
同样,在执行解密过程时,需要经过逆字节代替,因此也有相应的逆S盒,其代替方法与S盒完全相同。逆S盒与S盒是互逆的。
扩散层
扩散层由两个子层组成:ShiftRow变换和MixColumn变换。
ShiftRow子层
ShiftRow变换循环往复地将状态矩阵的第二行向左移动1个字节,将第三行向左移动2个字节,第四行向左移动3个字节。
MixColumn子层
这一步骤是一个线性变换,混淆状态矩阵的每一列。我们把长度为4字节的每列都看作一个向量,并且和一个固定的4*4矩阵相乘。此矩阵包含常量的向,系数的乘法和加法都在
密钥加法层
这一层,就是把16字节的当前状态矩阵与长度为16字节的子密钥进行异或。子密钥是通过密钥编排得到的。
密钥编排
密钥编排,将原始输入密钥作为输入,得到AES使用的子密钥。在AES的输入和输出中都使用了子密钥的XOR加法,这个过程有时称为密钥漂白(key whitening)。子密钥个数等于轮数加一,这是因为密钥加法层进行密钥漂白的时候也需要密钥,在之前的流程图中可以看到这一点。
AES的子密钥计算是递归的,即为了得到子密钥
下图是编排方式
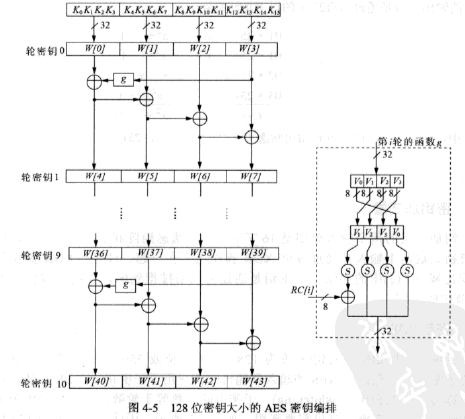
AES首先将初始密钥输入到一个1*4的状态矩阵中,这个矩阵的每一列的4个字节组成一个字,矩阵4列的4个字依次命名为W[0]、W[1]、W[2]和W[3],它们构成一个以字为单位的数组W。例如,设密钥K为"abcdefghijklmnop",则K0 = ‘a’,K1 = ‘b’, K2 = ‘c’,K3 = ‘d’,W[0] = “abcd”。
接着,对W数组扩充40个新列,构成总共44列的扩展密钥数组。新列以如下的递归方式产生:
-
若
不是4的倍数,那么第 列由如下等式确定 -
如果
是4的倍数,那么第 列由如下等式确定 其中,g是一个稍微复杂一些的函数。
函数
由3部分组成:字循环、字节代换和轮常量异或,这3部分的作用分别如下。 -
字循环:将1个字中的4个字节循环左移1个字节。即将输入字[b0, b1, b2, b3]变换成[b1,b2,b3,b0]。
-
字节代换:对字循环的结果使用S盒进行字节代换,S盒还是之前用到的那个。
-
轮常量异或:将前两步的结果同轮常量R[j]进行异或,其中j表示轮数。轮常量R[j]是一个字,其值见下表。
j 1 2 3 4 5 R[j] 01000000 02000000 04000000 08000000 10000000 j 6 7 8 9 10 R[j] 20000000 40000000 80000000 1B000000 36000000
在这里我们举个例子:
设初始的128位密钥为:
3C A1 0B 21 57 F0 19 16 90 2E 13 80 AC C1 07 BD
那么4个初始值为:下面求扩展的第1轮的子密钥(W[4],W[5],W[6],W[7])。
由于4是4的倍数,所以:的计算步骤如下: - 循环地将W[3]的元素移位:AC C1 07 BD变成C1 07 BD AC
- 将 C1 07 BD AC 作为S盒的输入,输出为78 C5 7A 91
- 将78 C5 7A 91与第一轮轮常量R[1]进行异或运算,将得到79 C5 7A 91,
因此,g(W[3])=79 C5 7A 91,故
W[4] = 3C A1 0B 21 ⨁ 79 C5 7A 91 = 45 64 71 B0其余的3个子密钥段的计算如下:
所以,第一轮的密钥为 45 64 71 B0 12 94 68 A6 82 BA 7B 26 2E 7B 7C 9B。
函数
的目的有两个,一个是增加密钥编排的非线性,另一个是消除AES中的对称性。 -
至此,我们介绍了加密的全过程。
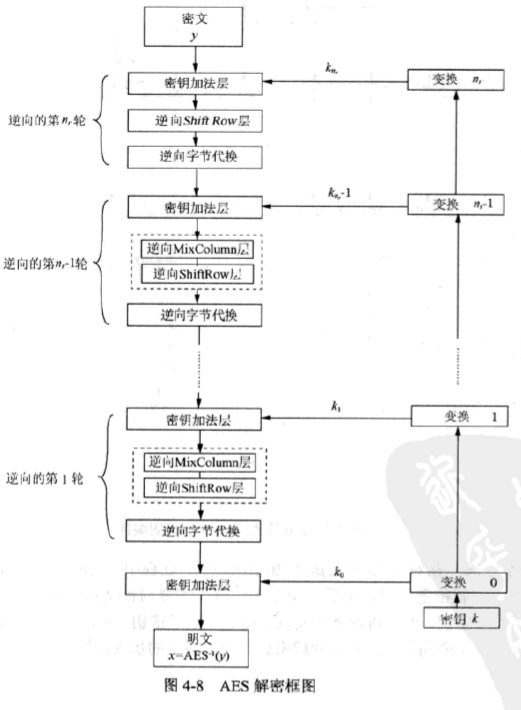
解密
解密过程需要把所有层都颠倒并且逆向,同时需要一个反向的子密钥编排。由于最后一轮加密没有MixColumn层,所以第一轮解密也不需要包含对应的逆层。
Sum
在本篇中,我们系统的学习了AES的加密过程,在下一篇中,我们会介绍分组密码的不同操作模式,这对于我们分析题目也有很大的帮助。




Comments NOTHING