Crypto CTF复现——1

由于当天在打巅峰极客，自己能力有限，双开不能，所以在比赛之后复现了。先复现了easy和medium easy的部分。

Symbols

题目图片是一些奇怪的符号，不过有些符号在Latex里面见过，所以去百度了一下latex符号输入，链接。然后对着符号一个个找，符号的第一个字母是我们需要的，最后拼接得到flag。

Keybase

阅读源码，我们可以知道，服务器可以给我们提供加密过后的flag，并且会用相同的key iv加密我们发送的数据，返回给我们key的前112位，以及加密的密文的后半部分。

很显然，这里key的后16位需要爆破，问题的关键在于，如何获得iv。

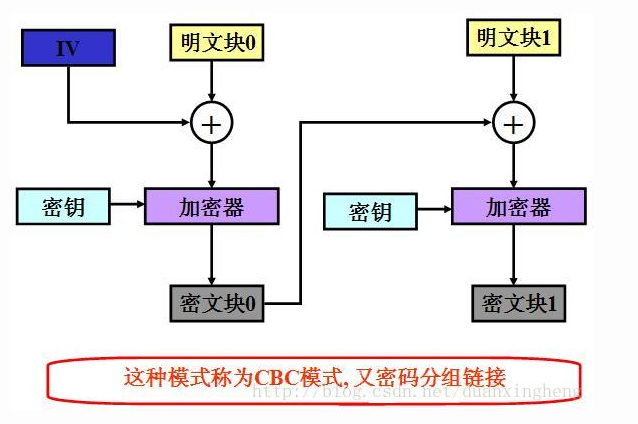
由CBC模式我们可以知道，对于我们发送的32字节明文，被分成了16字节的m0、m1，m0和iv异或后加密乘c0，c0和m1异或后加密得到c1。现在对于我们来说，首先需要把key爆破出来，这里我们用flag加密的密文c0做为iv，进行爆破。

from Crypto.Util.number import *
from Crypto.Cipher import AES
from string import printable
c = 0xb27e9095ded98a14bdb678e3a30fbbfc79b9cefc9a71b2c963804ce692e0b61e
c = long_to_bytes(c)
c1, c2 = c[:16], c[16:]
key = 0x52ab970fd21f2526aa74216300680000
for i in range(65536):
k = long_to_bytes(key + i)
aes = AES.new(k, AES.MODE_CBC, c1)
m2 = aes.decrypt(c2)
for j in m2:
if chr(j) not in printable:
break
else:
print(m2, k)
#b’_7He_5eCrET_1V?}’
#b’R\xab\x97\x0f\xd2\x1f%&\xaat!c\x00h\x86\xeb’

得到key之后，我们需要恢复iv。注意到对于加密前来说，iv/c0和明文块进行异或运算，实际上是等价的，所以我们只需要把m1作为iv，解密c1，就可以得到c0，再把m0作为iv，解密c0，就可以得到原来的iv。

key = b'R\xab\x97\x0f\xd2\x1f%&\xaat!c\x00h\x86\xeb'
c2 = long_to_bytes(0x531aec9dfc944f408d4df08e8f25aeaa)
aes = AES.new(key, AES.MODE_CBC, b'0' * 16)
c1 = aes.decrypt(c2)
aes = AES.new(key, AES.MODE_CBC, b'0' * 16)
iv = aes.decrypt(c1)
aes = AES.new(key, AES.MODE_CBC, iv)
print(aes.decrypt(c))

需要注意的是，每次的aes都需要重新设置，恢复初始状态。

farm

from sage.all import *
import string, base64, math
from flag import flag
ALPHABET = string.printable[:62] + ’\=’
F = list(GF(64))
def keygen(l):
key = [F[randint(1, 63)] for _ in range(l)]
key = math.prod(key) #Optimization the key length :D
return key
def maptofarm(c):
assert c in ALPHABET
return F[ALPHABET.index(c)]
def encrypt(msg, key):
m64 = base64.b64encode(msg)
enc, pkey = ”, key5 + key3 + key**2 + 1
for m in m64:
enc += ALPHABET[F.index(pkey * maptofarm(chr(m)))]
return enc
#KEEP IT SECRET
key = keygen(14) #I think 6414 > 264 is not brute-forcible :P
enc = encrypt(flag, key)
print(f’enc = {enc}’)

题目的加密很简单，就是两个多项式相乘，其中pkey是固定的，由于是在GF(64)域中，所以pkey只有64种情况，我们可以枚举，但是因为我们知道了flag的开头，所以可以直接计算出pkey。

import string, base64, math
enc = '805c9GMYuD5RefTmabUNfS9N9YrkwbAbdZE0df91uCEytcoy9FDSbZ8Ay8jj'
ALPHABET = string.printable[:62] + '\\='
F = list(GF(64))
fl=b'CCTF{'
def maptofarm(c):
    assert c in ALPHABET
    return F[ALPHABET.index(c)]
def encrypt(msg):
    m64 = base64.b64encode(msg)
    encr = ''
    for m in m64:
        encr += ALPHABET[F.index(maptofarm(chr(m)))]
    return encr
encr=encrypt(fl)
pkey=F[ALPHABET.index(enc[0])]/F[ALPHABET.index(encr[0])]
l=[]
for i in enc:
    l.append(F.index(F[ALPHABET.index(i)]/pkey))
print(l)
s=''
for i in l:
    s+=ALPHABET[i]
print(s)
print(base64.b64decode(s.encode()))

hamul

这题的RSA比较奇特

其中PP、QQ是由p、q字符串相加得到的，所以n的高位是p*q的高位，n的低位是p*q的低位。由于p、q位数很小，我们只需要把两端拼接在一起，并进行分解即可。

思路是这样的，但我们知道，数字相乘可能会有进位。对于我们得到的低位没有问题，但是对于高位来说，可能需要减去进位的数字，我们并不知道进了几，所以先从0-9开始，发现进1的时候，得到的数，刚好能分解成两个素数。在这之前，我们需要对p q的十进制位数进行估计，大约是19位或20位，先从19位开始，如果能出解就不需要考虑20位。

from Crypto.Util.number import *
import gmpy2
n = 98027132963374134222724984677805364225505454302688777506193468362969111927940238887522916586024601699661401871147674624868439577416387122924526713690754043
c = 42066148309824022259115963832631631482979698275547113127526245628391950322648581438233116362337008919903556068981108710136599590349195987128718867420453399
e = 65537
strn = str(n)
hn, ln = strn[:19], strn[len(strn) - 19:]
for i in range(10):
pq = int(hn+ln)-i*10**19
print(pq)
p = 9324884768249686093
q = 10512422984265378151
P = int(str(p) + str(q))
Q = int(str(q) + str(p))
PP = int(str(P) + str(Q))
QQ = int(str(Q) + str(P))
phi = (PP - 1) * (QQ - 1)
d = gmpy2.invert(e, phi)
print(long_to_bytes(pow(c, d, n)))

hyper_normal

这道题的源码实际上总结下来，就是矩阵运算

其中M是由明文*（i+1）得到的对角矩阵，打乱行或者列后得到的，但是我们知道，由于对角矩阵每行每列都只有一个数字，所以这并不改变明文原来的顺序。

而我们不知道R矩阵，不知道对应明文，所以我们需要对每个明文爆破，并且列出其和0-125相乘的所有值，如果给出的矩阵中有值不在其中，就可以否定这个明文。

from output import *
from string import printable
p = 8443
def transpose(x):
    result = [[x[j][i] for j in range(len(x))] for i in range(len(x[0]))]
    return result
M = transpose(M)
s = ''
for l in M:
    for m in printable:
        T = []
        count = 1
        for r in range(127):
            w=(ord(m)*(M.index(l)+1)*r)%p
            T.append(w)
        for t in l:
            if t not in T:
                count=0
        if count:
            s+=m
print(s)

Rima

这道题的关键就是要求出flag的长度，我自己是选择直接爆破的，不过好像有不爆破的方法，不清楚，有会的师傅教教我。别的地方在这题里都是可以逆的。

from Crypto.Util.number import *
import binascii
def to_base_5(n):
s = ”
while n:
s = str(n % 5) + s
n //= 5
return s
def nextPrime(n):
while True:
n += (n % 2) + 1
if isPrime(n):
return n
with open(‘g.enc’, ‘rb’) as f:
g_file = f.read()
g_long = bytes_to_long(g_file)
with open(‘h.enc’, ‘rb’) as f:
h_file = f.read()
h_long = bytes_to_long(h_file)
g_base5 = to_base_5(g_long)
h_base5 = to_base_5(h_long)
g_digits = [x for x in g_base5]
h_digits = [x for x in h_base5]
for i in range(7,50):
g=g_digits.copy()
h=h_digits.copy()
f_size = i * 8
a = nextPrime(f_size)
b = nextPrime(a)
c = nextPrime(f_size >> 2)
if len(g) < a * f_size + c:
g = [0] * (af_size+c - len(g)) + g
if len(h) < b * f_size + c:
h = [0] * (bf_size+c - len(h)) + h
g = [int(x) for x in g]
h = [int(x) for x in h]
for i in range(len(g) - c-1, -1, -1):
g[i] -= g[i+c]
for i in range(len(h) - c-1, -1, -1):
h[i] -= h[i+c]
if g[:c] != [0] * c or h[:c] != [0] * c:
continue
g = g[c:]
h = h[c:]
g = g[:f_size]
h = h[:f_size]
f = g
for i in range(len(f)-2, -1, -1):
f[i] -= f[i+1]
f = [str(x) for x in f]
f = int(”.join(f), 2)
f = hex(f)[2:]
print(f’MAYBE FLAG: {f}’)
try:
print(f’FLAG: {binascii.unhexlify(f)}’)
except:
continue