格归约算法
这一节我们会介绍LLL算法(终于到了)。在维度较小的情况下,LLL算法可以解决SVP以及CVP,但是当维度很大的时候,LLL算法就无能为力了。而现在基于格的密码系统的安全,就是建立在一系列格归约算法无法有效的解决apprSVP以及apprCVP之上的。
我们先说说二维的高斯格归约算法。

下面是实现代码
from Crypto.Util.number import *
from math import sqrt
def sgn(x):
if x==0:
return 0
if x>0:
return 1
if x<0:
return -1
def vecmul(veca,vecb):
assert len(veca)==len(vecb)
s=0
for i in range(len(veca)):
s+=veca[i]*vecb[i]
return s
def getans (veca,vecb):
print(veca,vecb)
if vecmul(vecb,vecb)<vecmul(veca,veca):
tmp=veca
veca=vecb
vecb=tmp
print(veca,vecb)
m=int(vecmul(veca,vecb)/vecmul(veca,veca)+0.5*sgn(vecmul(veca,vecb)))
if(m==0):
return veca,vecb
for i in range(len(vecb)):
vecb[i]-=m*veca[i]
return getans(veca,vecb)
a=[66586820,65354729]
b=[6513996,6393464]
A,B=getans(a,b)
print(A,B)
#[2280, -1001] [-1324, -2376]
LLL算法
高斯的晶格约简算法给出了在维数
现在我们有给定的格
在之前,我们提过下面这个不等式
其中
虽然我们知道,这样取得的正交基并不能保证每项都是整数,不能做
-
令
是格 的一组基, 是这组基正交化的结果。若 满足下面两个条件,就称其可被LLL规约。 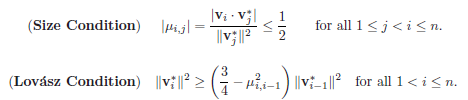
下面是LLL算法的具体过程:

由于LLL算法在Sagemath中已经自带了,这里就不放实现了。我们需要知道的是,LLL算法求出的矩阵,从上到下的向量长度依次增大,所以一般来说,要求的最短向量就是最上面一行的向量,不过也有特殊情况,让后面几行是可能解。
结语
至此,我们把格密码的知识了解了个大概,我终于把坑填了,当然有很多书中的知识和证明我没有摘录进来,如果以后有需要会补的(咕咕咕)。后面就可以利用格密码的知识进行解题了。


Comments NOTHING